matplotlibを使ってみた

Python プログラミング 地球科学

matplotlibというのはscipyに入っているグラフ描写用のライブラリです。普通は計算結果を適当なファイルに出力してそれでgnuplotなりで描写させるとおもうのですが、matplotlibを使えればPython一つでデータの解析から出力までできちゃいます。またPythonはネットワーク系のライブラリも充実しているのでデータサーバと通信してデータを落とすってとこまでできちゃいそうです(実際にやったわけではないんで実際にどういう感じにデータが配信されるとかはわからないのですが...)

さて地殻構造学(構造地質学の授業。岩石の変形とかの解析を扱う)で変形機構図の作成をする課題がでたのでせっかくなのでmatplotlibでやってみることにしました。
とりあえず教科書に乗っていたものを試しにやってみます。
今回の変形機構は転位クリープ(DLC)と粒界滑り(GBS)を扱っています。
それぞれの流動速が
\dot{e} = (\Delta \sigma)^{4.7} \exp(7.8 -\frac{298000}{8.3143T})
\dot{e} = \frac{(\Delta \sigma)^{1.7}}{d^3} \exp(15.3 -\frac{214000}{8.3143T})

と与えられています。この時T=673K(つまり400度)の条件で粒径と差応力の平面にプロットします。まずは値の範囲が広いので対数をとって両対数目盛でプロットするために適当に式変形します。また、卓越領域を求めるために歪み速度が等しくなる直線(両対数グラフ上で)を求めます。ここらへんは手計算で行いました。

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

#xの点列とyの点列(つまりGraph)を入れるための構造体的な
class Graph:
	pass

#Logをとった場合の転移クリープ(DLC)の差応力
def LogDLCDifferentialStress(LogStrainRate,GrainDiameter):
	return (LogStrainRate+19.746365)/4.7

#Logをとった場合の粒界滑り(GBS)の差応力
def LogGBSDifferentialStress(LogStrainRate,LogGrainDiameter):
	return (LogStrainRate+ 3*LogGrainDiameter+9.94823899)/1.7

#Logをとった場合のDLCとGBSの歪み速度が等しい点を結んだ直線
def LogEqualLine(GrainDiameter):
	return -GrainDiameter + 3.2730867

#軸の範囲(Log10)
xmin = 0
xmax = 3
ymin = 0
ymax = 3

#3つの図を作る
fig = plt.figure()
DLCFig = fig.add_subplot(221)
GBSFig = fig.add_subplot(222)
EqLineFig =fig.add_subplot(223)

for StrainRate in range(-6,-17,-1):
	#転移クリープのみのGraph
	DLC1 = Graph()
	DLC1.xs=np.arange(xmin,xmax,0.01)
	DLC1.ys=[LogDLCDifferentialStress(StrainRate, x) for x in DLC1.xs]

	DLCFig.plot(DLC1.xs,DLC1.ys,'k-')

	
	#粒界滑りのみのGraph
	GBS1 = Graph()
	GBS1.xs=np.arange(xmin,xmax,0.01)
	GBS1.ys=[LogGBSDifferentialStress(StrainRate, x) for x in GBS1.xs]
	GBSFig.plot(GBS1.xs,GBS1.ys,'k-')

	#変形機構図
	DLC2 = Graph()
	DLC2.xs=np.arange(xmin,LogEqualLine(LogDLCDifferentialStress(StrainRate, 0)),0.01)
	DLC2.ys=[LogDLCDifferentialStress(StrainRate, x) for x in DLC2.xs]

	GBS2 = Graph()
	GBS2.xs=np.arange(LogEqualLine(LogDLCDifferentialStress(StrainRate, 0)),xmax,0.01)
	GBS2.ys=[LogGBSDifferentialStress(StrainRate, x) for x in GBS2.xs]

	EqLineFig.plot(DLC2.xs,DLC2.ys,'k-')
	EqLineFig.plot(GBS2.xs,GBS2.ys,'k-')
	

#変形機構図の領域塗りつぶし
EqLine = Graph()
EqLine.xs=np.arange(xmin,xmax,0.01)
EqLine.ys=[LogEqualLine(x) for x in EqLine.xs]
EqLineFig.plot(EqLine.xs,EqLine.ys,'k-')
EqLineFig.fill_between(EqLine.xs, EqLine.ys, ymin , color='#ffcccc')
EqLineFig.fill_between(EqLine.xs, EqLine.ys, ymax , color='#ccccff')

#タイトル・余白の調整
fig.suptitle('deformation mechanism map')
fig.subplots_adjust(wspace = 0.30, hspace= 0.40)

#軸の調整
#GBSFig.set_title('deformation mechanism map')
GBSFig.set_xlabel('d($\mathrm{\mu m})$')
GBSFig.set_ylabel('$\Delta \sigma(\mathrm{M Pa})$')
GBSFig.axis([xmin,xmax,ymin,ymax])

GBSFig.set_xticks((1,2,3))
GBSFig.set_xticklabels(['$0$','$10$', '$10^2$','$10^3$'], size='15')
GBSFig.set_yticks((1,2,3))
GBSFig.set_yticklabels(['$0$','$10$', '$10^2$','$10^3$'], size='15')


DLCFig.set_xlabel('d($\mathrm{\mu m})$')
DLCFig.set_ylabel('$\Delta \sigma(\mathrm{M Pa})$')
DLCFig.axis([xmin,xmax,ymin,ymax])

DLCFig.set_xticks((1,2,3))
DLCFig.set_xticklabels(['$0$','$10$', '$10^2$','$10^3$'], size='15')
DLCFig.set_yticks((1,2,3))
DLCFig.set_yticklabels(['$0$','$10$', '$10^2$','$10^3$'], size='15')


EqLineFig.set_xlabel('d($\mathrm{\mu m})$')
EqLineFig.set_ylabel('$\Delta \sigma(\mathrm{M Pa})$')

EqLineFig.set_xticks((1,2,3))
EqLineFig.set_xticklabels(['$0$','$10$', '$10^2$','$10^3$'], size='15')
EqLineFig.set_yticks((1,2,3))
EqLineFig.set_yticklabels(['$0$','$10$', '$10^2$','$10^3$'], size='15')



#凡例
area1p = plt.Rectangle((0,0),1,1,fc='#ffcccc')
area2p = plt.Rectangle((0,0),1,1,fc='#ccccff')
EqLineFig.legend([area2p,area1p],["GBS","DLC"])
EqLineFig.axis([xmin,xmax,ymin,ymax])



#保存して終了
fig.savefig('simpleplot.png', dpi=96)

で、できた出力の図が
f:id:ikaro1192:20130102165859p:plain
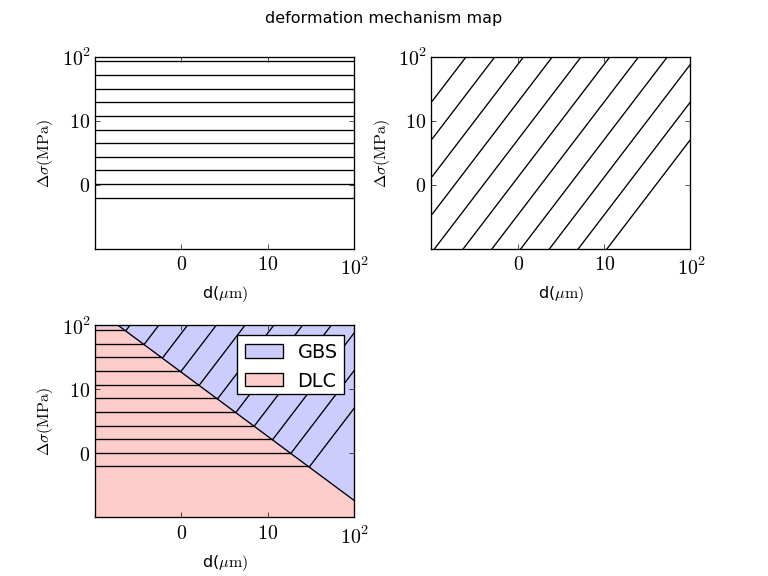
こんなかんじです。割と簡単にグラフが書けてしまいました。gnuplotみたいに技巧的なforやifを書かなくてもPythonの読みやすい構文で書けるというのも大きなメリットですね。scipyで数値計算した結果を...とかなるともっと有効に使えそうです。