友人とディスカッションしてきました。(まとめメモ)

思ったこと メモ

昨日は友人とディスカッションして来ました。
最初設定したテーマは「数学の新教育指導要領」について。特に「行列が廃止され、複素平面が導入されることについて」の話。
応用上行列はいたるところででてくるよね、とか複素平面をやらないと虚数が導入されてもイメージが湧きづらいという話とか。また、ちょっと話がずれて大学でテイラー展開を習った時に概念をさらっとだけれども知っていたので友人はすんなり理解できたが周りの人は全く知らなかったのでよくわかっていないようだったとか。やっぱり深くはしなくても知っていることは重要。だから軽くでも触れておいたほうがいいということに。
　それを考えた時に高校の段階で多くのことに触れておくことが重要なんじゃないか、また○○に使われているとか、別教科とのつながりがわかっているとやる気が出たり、するんじゃないかという話に。そういった時に高校でも総合的な学習の時間があると有意義なんじゃないか、特にいろいろな教科をやっている高校生の方が中学生よりも理解が深まるんじゃないかという話になりました。特に物理とかは微積を使わず逆に難易度が上がっている感じもしますし、数学でも不定積分から導入され面積としてイメージしやすいはずの積分がわかりにくくなっていたりとかそういうギャップを埋められるのではないかなと。
そんなこんなでやってるといつの間にかDiscussionの話になり、発表は出来る人はまあまあいるけど質疑応答がにがてなひとおおいよねってはなしになりました。
　そういった時に授業時間の問題があるだろうから、土曜日とかにそういう質疑応答も含めた、双方向的なフランクな感じでそういう授業があるといいよね～と。
　そんなこんな話しているうちに話しているだけでなにか行動起こせないかということに。これに関してはあまり結論が出ませんでした...自分たちだけで同行できる問題じゃないですし...ただ、何か行動を起こしていけば変わっていくのかもしれないなとも。

ベランダで起きた怪奇現象

地球科学 雑記

タイトルは半分釣りですｗ

今朝母がベランダを見ると雪の溶け残った跡のところに土が散乱しているとのこと。
f:id:ikaro1192:20130119101957j:plain
最初は花壇からこぼれたのではないかとか思い見てみましたが、写真のように平らです。
f:id:ikaro1192:20130119102005j:plain
ここは三階なので風で飛ばされたようにも思えませんしどこからこの土はきたのでしょうか?
答えは雪の溶け残った跡というところにありました。土を手にとってみてみると塊になっている。下に霜柱が入っていて、それと雪とがかたまり、土がサンドイッチされる形になっていたっぽいのです。(この写真だとだいぶ溶けてしまっていてわかりにくいですが...)
f:id:ikaro1192:20130119102017j:plain
鼻に聞いてみると幸がいっぱい残っていたのでベランダの方に避けておいたとのこと。つまり、気づかずに雪と一緒に霜柱と土塊を運んでしまっていたわけですね。超自然現象でもなんでもなく母が気づかずに運んだだけだったとは...
一応授業で霜柱とかで石が運ばれる現象とかやっていますけど、実際見ると(今回は完全に自然というわけではないですが)違いますね。

新年の抱負(いまさら)

いまさらですね。でも書かないよりはマシということで書いておきますｗ

まずは勉強関連ですと物理数学・地学のための物理のようなサイトのコンテンツを作ろうとか考えています。とくに前者はあまりこういうサイトではできるものとして扱われてない初等関数の説明、数列、微積分とか高校の範囲から説明始めようかなと。たぶん、わたしの説明で役に立つのはレポートに追われていて答えさえ出ればいい大学生よりは自分で勉強したいけど、どこから手をつけていいのかわからない(わたしのような)人のほうでしょうから。

プログラミング関係ではRPG製作を個人で再開しようかと。素材とかどうするの?とかは今後考えます。設計自体はできているのでコーディングするだけなはず。どんだけかかるかわかりませんが、少なくとも自分だけなら前にすすめるでしょうとかおもったり。
　あとは数値計算あたりにももうちょっとしっかり手を出してみようかと。
　ついでにwebでDjangoあたりもまともに触りたいです。
忘れちゃいけないのが、サークルの方で作っているSTGですね。まあ、こっちはサポートという形なので適当に(適切にって意味ですよ!)やっていこうかと。

ということでこんなわたしですが、今年もよろしくお願いします。

matplotlibを使ってみた

Python プログラミング 地球科学

matplotlibというのはscipyに入っているグラフ描写用のライブラリです。普通は計算結果を適当なファイルに出力してそれでgnuplotなりで描写させるとおもうのですが、matplotlibを使えればPython一つでデータの解析から出力までできちゃいます。またPythonはネットワーク系のライブラリも充実しているのでデータサーバと通信してデータを落とすってとこまでできちゃいそうです(実際にやったわけではないんで実際にどういう感じにデータが配信されるとかはわからないのですが...)

さて地殻構造学(構造地質学の授業。岩石の変形とかの解析を扱う)で変形機構図の作成をする課題がでたのでせっかくなのでmatplotlibでやってみることにしました。
とりあえず教科書に乗っていたものを試しにやってみます。
今回の変形機構は転位クリープ(DLC)と粒界滑り(GBS)を扱っています。
それぞれの流動速が
\dot{e} = (\Delta \sigma)^{4.7} \exp(7.8 -\frac{298000}{8.3143T})
\dot{e} = \frac{(\Delta \sigma)^{1.7}}{d^3} \exp(15.3 -\frac{214000}{8.3143T})

と与えられています。この時T=673K(つまり400度)の条件で粒径と差応力の平面にプロットします。まずは値の範囲が広いので対数をとって両対数目盛でプロットするために適当に式変形します。また、卓越領域を求めるために歪み速度が等しくなる直線(両対数グラフ上で)を求めます。ここらへんは手計算で行いました。

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

#xの点列とyの点列(つまりGraph)を入れるための構造体的な
class Graph:
	pass

#Logをとった場合の転移クリープ(DLC)の差応力
def LogDLCDifferentialStress(LogStrainRate,GrainDiameter):
	return (LogStrainRate+19.746365)/4.7

#Logをとった場合の粒界滑り(GBS)の差応力
def LogGBSDifferentialStress(LogStrainRate,LogGrainDiameter):
	return (LogStrainRate+ 3*LogGrainDiameter+9.94823899)/1.7

#Logをとった場合のDLCとGBSの歪み速度が等しい点を結んだ直線
def LogEqualLine(GrainDiameter):
	return -GrainDiameter + 3.2730867

#軸の範囲(Log10)
xmin = 0
xmax = 3
ymin = 0
ymax = 3

#3つの図を作る
fig = plt.figure()
DLCFig = fig.add_subplot(221)
GBSFig = fig.add_subplot(222)
EqLineFig =fig.add_subplot(223)

for StrainRate in range(-6,-17,-1):
	#転移クリープのみのGraph
	DLC1 = Graph()
	DLC1.xs=np.arange(xmin,xmax,0.01)
	DLC1.ys=[LogDLCDifferentialStress(StrainRate, x) for x in DLC1.xs]

	DLCFig.plot(DLC1.xs,DLC1.ys,'k-')

	
	#粒界滑りのみのGraph
	GBS1 = Graph()
	GBS1.xs=np.arange(xmin,xmax,0.01)
	GBS1.ys=[LogGBSDifferentialStress(StrainRate, x) for x in GBS1.xs]
	GBSFig.plot(GBS1.xs,GBS1.ys,'k-')

	#変形機構図
	DLC2 = Graph()
	DLC2.xs=np.arange(xmin,LogEqualLine(LogDLCDifferentialStress(StrainRate, 0)),0.01)
	DLC2.ys=[LogDLCDifferentialStress(StrainRate, x) for x in DLC2.xs]

	GBS2 = Graph()
	GBS2.xs=np.arange(LogEqualLine(LogDLCDifferentialStress(StrainRate, 0)),xmax,0.01)
	GBS2.ys=[LogGBSDifferentialStress(StrainRate, x) for x in GBS2.xs]

	EqLineFig.plot(DLC2.xs,DLC2.ys,'k-')
	EqLineFig.plot(GBS2.xs,GBS2.ys,'k-')
	

#変形機構図の領域塗りつぶし
EqLine = Graph()
EqLine.xs=np.arange(xmin,xmax,0.01)
EqLine.ys=[LogEqualLine(x) for x in EqLine.xs]
EqLineFig.plot(EqLine.xs,EqLine.ys,'k-')
EqLineFig.fill_between(EqLine.xs, EqLine.ys, ymin , color='#ffcccc')
EqLineFig.fill_between(EqLine.xs, EqLine.ys, ymax , color='#ccccff')

#タイトル・余白の調整
fig.suptitle('deformation mechanism map')
fig.subplots_adjust(wspace = 0.30, hspace= 0.40)

#軸の調整
#GBSFig.set_title('deformation mechanism map')
GBSFig.set_xlabel('d($\mathrm{\mu m})$')
GBSFig.set_ylabel('$\Delta \sigma(\mathrm{M Pa})$')
GBSFig.axis([xmin,xmax,ymin,ymax])

GBSFig.set_xticks((1,2,3))
GBSFig.set_xticklabels(['$0$','$10$', '$10^2$','$10^3$'], size='15')
GBSFig.set_yticks((1,2,3))
GBSFig.set_yticklabels(['$0$','$10$', '$10^2$','$10^3$'], size='15')


DLCFig.set_xlabel('d($\mathrm{\mu m})$')
DLCFig.set_ylabel('$\Delta \sigma(\mathrm{M Pa})$')
DLCFig.axis([xmin,xmax,ymin,ymax])

DLCFig.set_xticks((1,2,3))
DLCFig.set_xticklabels(['$0$','$10$', '$10^2$','$10^3$'], size='15')
DLCFig.set_yticks((1,2,3))
DLCFig.set_yticklabels(['$0$','$10$', '$10^2$','$10^3$'], size='15')


EqLineFig.set_xlabel('d($\mathrm{\mu m})$')
EqLineFig.set_ylabel('$\Delta \sigma(\mathrm{M Pa})$')

EqLineFig.set_xticks((1,2,3))
EqLineFig.set_xticklabels(['$0$','$10$', '$10^2$','$10^3$'], size='15')
EqLineFig.set_yticks((1,2,3))
EqLineFig.set_yticklabels(['$0$','$10$', '$10^2$','$10^3$'], size='15')



#凡例
area1p = plt.Rectangle((0,0),1,1,fc='#ffcccc')
area2p = plt.Rectangle((0,0),1,1,fc='#ccccff')
EqLineFig.legend([area2p,area1p],["GBS","DLC"])
EqLineFig.axis([xmin,xmax,ymin,ymax])



#保存して終了
fig.savefig('simpleplot.png', dpi=96)

で、できた出力の図が
f:id:ikaro1192:20130102165859p:plain
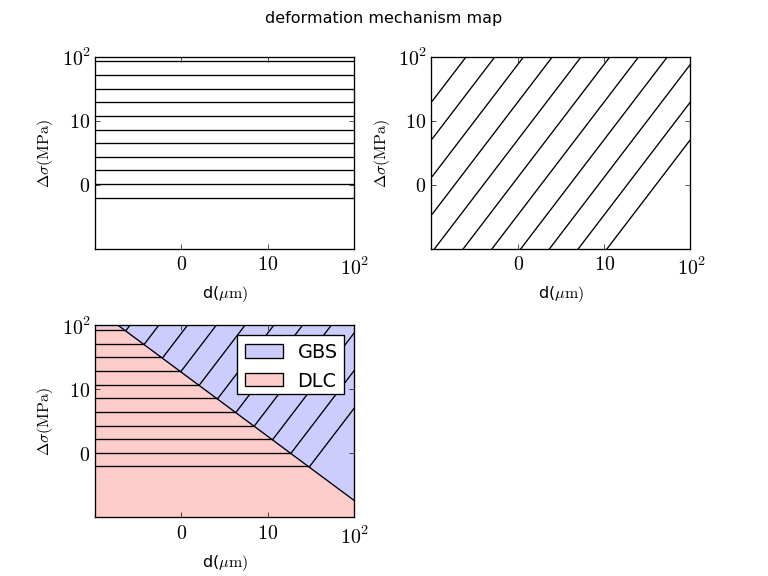
こんなかんじです。割と簡単にグラフが書けてしまいました。gnuplotみたいに技巧的なforやifを書かなくてもPythonの読みやすい構文で書けるというのも大きなメリットですね。scipyで数値計算した結果を...とかなるともっと有効に使えそうです。

(x-a)(x-b)の平方完成の公式

数学 メモ

レポート書いていたら見つけたのでメモ。
(x-a)(x-b)の平方完成だが、これは
(x-a)(x-b) = (x-\frac{a+b}{2})^2 + (\frac{b-a}{2})^2
という風にできる。和と差で書けるということで割りと覚えやすいと思う。aとbが複雑な文字式で展開してそれを平方完成する必要に迫られた時とかに有効。普通の平方完成をする必要がある問題でも因数分解が簡単なら簡単にできるかもしれない。
　さて証明だ。
(x-a)(x-b)
= (x-\frac{a+b}{2}+\frac{b-a}{2})(x-\frac{a+b}{2}-\frac{b-a}{2})
= (x-\frac{a+b}{2})^2 + (\frac{b-a}{2})^2
となる。二番目の式でうまく\frac{a+b}{2}が出てくるように式変形してあげると (X+A)(X-A)の形が出てくるのであとは公式に従って展開すればいいだけだ。ここがちょっとトリッキーかもしれないが答えにたどり着くことを信じて希望的観測で式変形するのは常套手段だと思う。世の中は大体うまく行くようにできてる。

応用としてこれからx^2+bx+cの平方完成をしてみよう。これを=0とおいて二次方程式とみなした時の解をα,βとすれば
x^2+bx+c=(x-\alpha)(x-\beta)
ここで右辺に公式を適応して
= (x-\frac{\alpha+\beta}{2})^2 + (\frac{\beta-\alpha}{2})^2
解と係数の関係より
\alpha+\beta = -b
また、判別式Dは
D=\sqrt{ b^2 -4c} =\beta-\alpha
なのでこれを代入して
= (x+\frac{b}{2})^2 + (\frac{\sqrt{ b^2 -4c}}{2})^2
= (x+\frac{b}{2})^2 + \frac{b^2 -4c}{4}
となる。とわりと簡単に導出できた。
なお、判別式の部分はD^2は対称式になることから解と係数の関係から求められるが、今回はやらない。

暗黙の型変換を禁止するテンプレートクラス

C++ プログラミング

暗黙の型変換はときおり悩まされる。しかも、コンパイラは警告すら出さない。
　先日複数の引数がある関数をつくり、それでint型とbool型を受け取っていた。この場合型が異なるし独自の型を導入しなくてもいいだろうとか思っていたのが間違いだった。int型の変数にboolの値を代入するときエラーは愚か警告すら出ずしばらく悩んでいた。
ようするに以下のコードがコンパイルを通ってしまうのだ。

int main(){
    int hoge =true;
}

これは非常に気持ち悪い。ということでこれを禁止するために以下のようなテンプレートクラスを書いた。

template<typename T>
class StrictType{
public:
	template<typename U>
	StrictType(U){
		static_assert(false, "bad cast");
	}

	template<>
	StrictType<T>(T obj):
		data(obj)
	{}

	operator T() const{return data;}

private:
	const T data;


};

変換コンストラクタをテンプレートメンバ関数にしてオーバーライドにより条件分岐している。テンプレートのほうが呼ばれた場合、テンプレートversionのメンバ関数が生成されるのでそこでstatic_assertでエラーを吐くというわけだ。
　実際に使う時は合理的に見える継承関係にあるクラスとかポインタの処理を加えたほうがいいかもしれない。あと変換関数をもっと何とかしたい...

二成分系の相図[連続固溶体が平衡結晶する場合]

メモ 地球科学

授業でやったのでまとめとして書いておきます。

まずは例として連続固溶体から。連続的固溶体というのは連続的にある成分が置き換わっていく固溶体のことです。

例として曹長石(albite)と灰長石(anorthite)の固溶体、つまり斜長石(plagioclases)について考えます。カルシウムにとむ斜長石が曹長石、ナトリウムにとむ斜長石が灰長石というわけですね。

(i)平衡結晶
まずはゆっくりと平衡状態をたもちながら結晶化することを考えます。例として図のXの組成と温度のmeltを冷やすことを考えましょう。この状態ではLq、つまり液体の領域にあるので当然(Ab:An)=(a:b)の組成を持つ液体ということになります。これを組成を変えないまま(変わる理由も無いですから)温度を下げていきます。そうするとT1の温度でLiquidus(液相線)とぶつかります(図のA点)。Liquidus上というのは液体が固体にちょうど変わる境界線、あるいは液体と固体が共存している領域となります。どうようにSolidus上というのは固体が液体ちょうど変わる境界線、あるいは液体と固体が共存している領域となります。相図の概略をしめしたものが上側の図になります。
f:id:ikaro1192:20121219225919j:plain
ではこのときでてくる固体の組成はどうなるでしょうか?相図上(下の相図)ではT1でかつ固体の領域となります。さらに制限条件として忘れていけないのが液体と固体が共存できる領域です。そうなるとT1とSolidusがぶつかるところ(図のA'点)ということになります。さて、ここでおもしろいことが起こっています。Xの組成から出発したのにそれとは異なる組成の固体ができています。連続固溶体が結晶化してでてくるのはつねにXとおなじせいぶんのものではないんですね。さて、ここで困ったことが起きます。物質の出入りがないわけですから全体の組成(つまり液体と固体全部を合わせた成分)はつねにXのはずです。ところが、XよりAnに富む固体ができてしまいました。これでは辻褄が合いません。そこでmeltの方の組成はそれを補うようにAbが増える方向に変化します。これはAnは固体の方に入りやすく、Abは液体に残りやすい考えることができますね。
さて、そのあと相図上ではmeltの組成と温度は液相線にそってAbのほうに向かいます。一方それにともなってでてくる固体の方は固相線にそって変化していきます。このまますすんでいくとちょうどBまで来た時(温度がT2になったとき)すべてが固体になることがわかります。(全体の組成としてはXなので固体の組成がXになったとということはもうmeltは残っていないので)こうして最終的にXの組成の固体ができて終わりです。
と、このように単純な二成分の理想的条件下の結晶化を考えただけでもいろいろな組成のけっしょうができることが理解できますね。